Question

In college basketball, some teams get most of their points from just one player, and other teams are more balanced in scoring. Consider the following facts about the scoring distributions for some NCAA Division I basketball teams. Each team has 121212 players. At Baylor University, there are 666 players who each score 121212 points per game, and there are 666 players who each score 000 points per game. At the University of Maryland, one player scores 585858 points per game, one player scores 141414 points per game, and the rest of the players score 000 points per game. At Dartmouth College, 444 players score 555 points per game, 444 players score 666 points per game, and 444 players score 777 points per game. Which of the following is true? Choose all answers that apply:

A) At Dartmouth, the mean number of points per player per game is greater than the median number of points per player per game.

B) At Maryland, the mean number of points per player per game is greater than the median number of points per player per game.

C) The median number of points per player per game is the same at all 333 schools.

D) The mean number of points per player per game is the same at all 333 schools.

Answer 1

b

Explanation:

Answer 2

B) At Maryland, the mean number of points per player per game is greater than the median number of points per player per game.

Explanation:

Baylor University

There are 6 players who each score 12 points per game.

There are 6 players who each score 0 points per game.

The Points of the 12 players are: 0,0,0,0,0,0,6,6,6,6,6,6

`Mean=(0*6+6*6)/(12) =3\\Median=0`

University of Maryland

One player scores 58 points per game,

One player scores 14 points per game,

The rest(10) of the players score 0 points per game.

The Points of the 12 players are: 0,0,0,0,0,0,0,0,0,0,14,58

`Mean=(14+58)/(12)= 6\\Median=0`

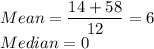
Dartmouth College

4 players score 5 points per game.

4 players score 6 points per game.

4 players score 7 points per game.

The Points of the 12 players are: 5,5,5,5,6,6,6,6,7,7,7,7

`Mean=(5*4+6*4+7*4)/(12) =6\\Median=(6+6)/(2) =6`

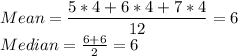
The following therefore applies:

B) At Maryland, the mean number of points per player per game is greater than the median number of points per player per game.