Complete Question
One day, after pulling down your window shade, you notice that sunlight is passing through a pinhole in the shade and making a small patch of light on the far wall. Having recently studied optics in your physics class, you're not too surprised to see that the patch of light seems to be a circular diffraction pattern. It appears that the central maximum is about 2 cm across, and you estimate that the distance from the window shade to the wall is about 5 m.
Required:
Estimate the diameter of the pinhole.
Answer:
The diameter is

Step-by-step explanation:
From the question we are told that
The central maxima is
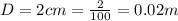
The distance from the window shade is
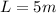
The average wavelength of the sun is mathematically evaluated as
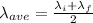
Generally the visible light spectrum has a wavelength range between 400 nm to 700 nm
So the initial wavelength of the sun is
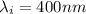
and the final wavelength is
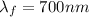
Substituting this into the above equation

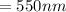
The diameter is evaluated as
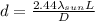
substituting values

