Question

In a Young’s interference experiment, the two slits are separated by 0.150 mm and the incident light includes two wavelengths: l1 5 540 nm (green) and l2 5 450 nm (blue). The overlapping interference patterns are observed on a screen 1.40 m from the slits. Calculate the minimum distance from the center of the screen to a point where a bright fringe of the green light coincides with a bright fringe of the blue light:_____

Answer 1

2.52 × 10⁻² cm

Step-by-step explanation:

The distance of bright fringe from the center of the screen is given by the formula

`y = (m\lambda D)/(d)`

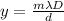
Here, wavelength is λ, Distance of the screen from the slits is D, seperation between the

slits is d.

Separation between the slits, d = 0.15 mm

`= 0.15 * 10^(-3) m`

Distance of the screen from the slits = 1.40 m

We have a wavelength, λ1 = 540 nm

=
`540 * 10^(-9) m`

By substituting all these values in the above equation we get

y1 = mλD/d

`y1 = m(540 * 10^(-9) m)(1.40 m)/(0.15 * 10^(-3) m)`

`y1 = m(5.04 * 10^(-3) m)`

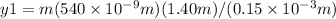
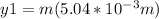
We have a wavelength, λ2 = 450 nm

=
`450 * 10^-9 m`

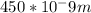
By substituting all these values in the above equation we get

`y_2 = (m\lambda D)/(d)`

`y_2 = m(450 * 10^(-9) m)(1.40 m)/(0.15 * 10^(-3) m)`

`y_2 = m'(4.20 * 10^(-3) m)`

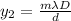
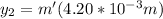
According to the problem, these two distance are coincides with each other.

So,

`y_1 = y_2`

`m(5.04 * 10^(-3) m) = m'(4.20 * 10^(-3) m)`

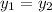
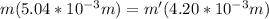
by testing values, the above equation is satisfied only when, m = 5 and m' = 6

Then from the above we have

y1 = y2 = 0.0252 m

= 2.52 × 10⁻² cm