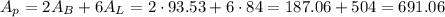1 Answer

Kiee · Answer 1 · 2021-09-18T22:05:42+0000

Answer:

The surface area of a regular hexagonal prism has a base edge of 6 feet and a lateral edge of 14 feet is A_p=691.06 ft^2.

Explanation:

The surface area for a regular hexagonal prism consist of the sum of two bases and six lateral faces.

The area of the base is calculated dividing the surface in six equal triangles, one for each edge of the base and later adding the individual areas.

The triangles obtained are equilateral, with angles of 60 degrees.

The area of a triangle of this type is:

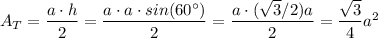
$A_T=(a\cdot h)/(2)=(a\cdot a\cdot sin(60^(\circ)))/(2)=(a\cdot (√(3)/2)a)/(2)=(√(3))/(4)a^2$

Then, the area for the base is the sum of 6 of this triangles area:

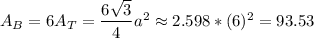
$A_B=6A_T=(6√(3))/(4)a^2\approx2.598*(6)^2=93.53$

The area of the lateral face is calculated as:

$A_L=a\cdot b=6\cdot 14=84$

Then, the surface area for the prism is:

$A_p=2A_B+6A_L=2\cdot93.53+6\cdot84=187.06+504=691.06$

Please log in or register to add a comment.