Question

What are the solutions of the equation (x + 2)2 + 12(x + 2) – 14 = 0? Use u substitution and the quadratic formula to solve. x = negative 8 plus-or-minus 5 StartRoot 2 EndRoot x = negative 6 plus-or-minus 5 StartRoot 2 EndRoot x = negative 4 plus-or-minus 5 StartRoot 2 EndRoot x = negative 2 plus-or-minus 5 StartRoot 2 EndRoot

Answer 1

B.
`x = -6 +/- 2√(5)`

Explanation:

substitute u for (x+2)

`u^2+12u -14=0`

use the quadratic formula

`\frac{-b plus-or-minus \sqrt{b^(2)- 4ac } }{2a}`

`(-12 plus-or-minus √(200) )/(2)`

`(-12 plus-or-minus 10√(2) )/(2)`

Then set everything equal to u: (x+2)

`u+2=(-12 plus-or-minus 10√(2) )/(2)`

u-2= -12 plus-or-minus 10 sqrt{2}/2

Answer 2

The solutions of the quadratic equation
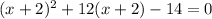`\((x + 2)^2 + 12(x + 2) - 14 = 0\)` are
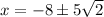`\(x = -8 \pm 5√(2)\)`, corresponding to option A.

Let's solve the given quadratic equation
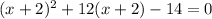`\((x + 2)^2 + 12(x + 2) - 14 = 0\)` using the u substitution method and then the quadratic formula.

1. u substitution:

Let u = x + 2, then the equation becomes
`\(u^2 + 12u - 14 = 0\)`.

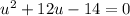2. Quadratic formula:

The quadratic formula is given by
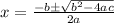`\(x = (-b \pm √(b^2 - 4ac))/(2a)\)`, where the quadratic equation is in the form
`\(ax^2 + bx + c = 0\)`.

For our equation
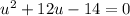`\(u^2 + 12u - 14 = 0\)`, the coefficients are a = 1, b = 12, and c = -14.

Applying the quadratic formula:

`\[u = (-12 \pm √(12^2 - 4(1)(-14)))/(2(1))\] \[u = (-12 \pm √(144 + 56))/(2)\] \[u = (-12 \pm √(200))/(2)\] \[u = (-12 \pm 10√(2))/(2)\] \[u = -6 \pm 5√(2)\]`

3. Substitute back u = x + 2:

`\[x + 2 = -6 \pm 5√(2)\] \[x = -8 \pm 5√(2)\]`

Now, let's check the answer choices:

A.
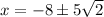`\(x = -8 \pm 5√(2)\)` - matches our result.

B.
`\(x = -6 \pm 5√(2)\)` - does not match.

C.
`\(x = -4 \pm 5√(2)\)` - does not match.

D.
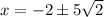`\(x = -2 \pm 5√(2)\)` - does not match.

So, the correct answer is A.
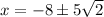`\(x = -8 \pm 5√(2)\)`.