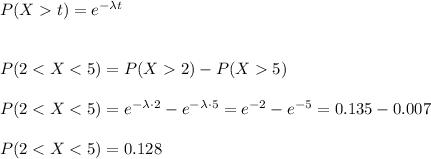Question

Let X = the time between two successive arrivals at the drive-up window of a local bank. If X has an exponential distribution with λ = 1, (which is identical to a standard gamma distribution with α = 1), compute the following. (a) The expected time between two successive arrivals

(b) The standard deviation of the time between successive arrivals
(c) P(X ? 1)
(d) P(2 ? X ? 5)

Answer 1

a) E(X)=1

b) σ=1

c) P(X>1)=0.368

d) P(2<X<5)=0.128

Explanation:

We have X: "the time between two successive arrivals at the drive-up window of a local bank", exponentially distributed with λ = 1.

a) We have to compute the expected time between two successive arrivals.

The expected value for X as it is exponentially distributed is:

`E(X)=(1)/(\lambda)=(1)/(1)=1`

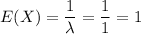
b) We have to compute the standard deviation of X.

The standard deviation is calculated as:

`\sigma=(1)/(\lambda)=(1)/(1)=1`

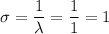
c) The probability that X is larger than 1 (P(X>1))

We can express the probability as:

`P(X>t)=e^(-\lambda t)\\\\P(X>1)=e^(-\lambda\cdot 1)=e^(-1)=0.368`

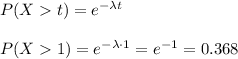
d) The probability that X is between 2 and 5 (P(2<X<5))

`P(X>t)=e^(-\lambda t)\\\\\\P(2<X<5)=P(X>2)-P(X>5)\\\\P(2<X<5)=e^(-\lambda\cdot 2)-e^(-\lambda\cdot 5)=e^(-2)-e^(-5)=0.135-0.007\\\\P(2<X<5)=0.128`