Question

A physiologist believes he has discovered a new steroid hormone that can control the blood glucose in mammals. In an experiment he injects laboratory rats with a small amount of this putative steroid hormone and, after a suitable waiting period measures the blood glucose level of the rats. In his twelve experimental rats he obtains the following levels of blood glucose {35,36,37,33,34,35,33,35,37,36,34,35}. From previous studies of thousands of normal, un-manipulated rats he knows that the mean (?) blood glucose level in this species of rat (his laboratory population) is 31 and that the standard deviation (?) is 4.12. Use a Z-test to evaluate the directional hypothesis that this new steroid hormone decreases blood glucose levels. Use an alevel of 0.05 for this analysis.

A) what is the null hypothesis?
B) what is the alternative hypothesis?
C) what is the critical value with and alpha of .05?
D) what is Z obt?
E) what should the cognitive psychologist conclude?

Answer 1

The null hypothesis states no effect of the steroid on glucose levels (mean ≥31), while the alternative suggests the steroid decreases levels (mean < 31). The critical Z-value for α = 0.05 in a one-tailed test is -1.645. The computed Z-score (3.49) exceeds the critical value, leading to rejection of the null hypothesis, indicating the new steroid likely decreases glucose levels.

Step-by-step explanation:

To answer the student's question about evaluating the hypothesis that a new steroid hormone decreases blood glucose levels using a Z-test, we need to follow these steps:

State the null and alternative hypotheses:

• Null Hypothesis (H0): The mean blood glucose level after the injection is ≥31 (the effect of the new steroid is not to decrease blood glucose levels).
• Alternative Hypothesis (H1): The mean blood glucose level after the injection is < 31 (the new steroid does decrease blood glucose levels).

Find the critical value for α = 0.05. Since this is a one-tailed test, we use Z-tables or a statistical program to find the Z-score that corresponds to the 95% percentile.

• Critical value (Zα) = -1.645 for a one-tailed test at α = 0.05.

Calculate the Z obtained (Zobt) using the formula Z = (X - μ) / (σ/√n), where X is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.

• First, find the mean of the sample data: (35+36+37+33+34+35+33+35+37+36+34+35) / 12 = 35.
• Then, calculate Zobt: Z = (35 - 31) / (4.12/√12) = 4 / (4.12/√12) ≈ 3.49.

Make a conclusion by comparing the Zobt to the critical value.

• Since 3.49 > -1.645, we reject the null hypothesis.

Thus, there is sufficient evidence to support the alternative hypothesis that the new steroid decreases blood glucose levels.

Answer 2

(a) H₀: μ = 31.

(b) Hₐ: μ < 31.

(c) The critical value of z at α = 0.05 is -1.645.

(d) The test statistic is 3.36.

(e) The cognitive psychologist should conclude that the new steroid hormone does not decreases the blood glucose levels.

Step-by-step explanation:

In this scenario, we need to determine whether the new steroid hormone decreases blood glucose levels.

A physiologist injects 12 laboratory rats with a small amount of this putative steroid hormone and, after a suitable waiting period measures the blood glucose level of the rats.

The data provided is:

S = {35, 36, 37, 33, 34, 35, 33, 35, 37, 36, 34, 35}

Compute the sample mean as follows:

`\bar x=(1)/(n)\sum X_(i)`

`=(1)/(12)* [35+36+37+33+34+35+33+35+37+36+34+35]\\=35`

Also it is given that:

μ = 31

σ = 4.12

(a)

The null hypothesis for this test can be defined as:

H₀: The new steroid hormone does not decreases the blood glucose levels, i.e. μ = 31.

(b)

The alternate hypothesis for this test can be defined as:

Hₐ: The new steroid hormone decreases the blood glucose levels, i.e. μ < 31.

(c)

The critical value of the distribution is the value beyond which the rejection region lies.

In this case we will use the z-test for single, since the population standard deviation is known.

The critical value of z at α = 0.05 is:

`z_(\alpha)=z_(0.05)=-1.645`

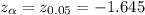
*Use a z-table.

The negative value is because of the alternate hypothesis, i.e. since we need the mean to be less than 31, the rejection region will be at μ < 31.

Thus, the critical value of z at α = 0.05 is -1.645.

(d)

Compute the value of the test statistic as follows:

`z=(\bar x-\mu)/(\sigma/√(n))=(35-31)/(4.12/√(12))=3.36`

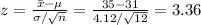
The test statistic is 3.36.

(e)

The test statistic value, z = 3.36 > z₀.₀₅ = -1.645.

The null hypothesis was failed to be rejected.

Thus, the cognitive psychologist should conclude that the new steroid hormone does not decreases the blood glucose levels.