Question

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is measured in millimeters. The results of the samples are presented next.

Process A: Sample Mean= 2.0, Standard Deviation= 1.0, Sample Size= 12
Process B: Sample Mean= 3.0, Standard Deviation= 0.5, Sample Size= 14
The researcher is interested in determining whether there is evidence that the two processes yield different average errors. The population standard deviations are unknown but are assumed equal.
Answer the following:
A. Assume you are trying to conclude if the two processes yield different average errors. Determine if the appropriate hypothesis test should be an upper tail, lower tail, or 2-tail test.
B. Determine the value of the test statistic.
C. Determine the critical z or t value using a level of significance of 5%.
D. Determine the p-value.
E. State your conclusion: Reject H0 or Do not Reject H0? (Using a significance level of 5%).
F. What is the probability of making a Type I Error?

Answer 1

A. As we are trying to test if the two processes yield different average errors, we are interested in any of the two posibilities: the average error of process A being statistically significant lower or bigger than the average error of Process B. That is why this is a two-tailed test.

B. t=-3.144

C. The critical value for a significance level of 0.05, a two tailed test with 4 degrees of freedom is t=±2.064.

D. P-value = 0.004

E. Reject H0

F. The probability of making a Type I error is equal to the significance level: P(Type I error) = 0.05.

Explanation:

This is a hypothesis test for the difference between populations means.

The claim is that the two processes yield different average errors.

As we are trying to test if the two processes yield different average errors, we are interested in any of the two posibilities: the average error of process A being statistically significant lower or bigger than the average error of Process B. That is why this is a two-tailed test.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2\\eq 0`

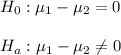
being μ1: average error for Process A and μ2: average error fo Process B.

The significance level is 0.05.

The sample 1, of size n1=12 has a mean of 2 and a standard deviation of 1.

The sample 1, of size n1=14 has a mean of 3 and a standard deviation of 0.5.

The difference between sample means is Md=-1.

`M_d=M_1-M_2=2-3=-1`

The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(1^2)/(12)+(0.5^2)/(14)}\\\\\\s_(M_d)=√(0.083+0.018)=√(0.101)=0.318`

Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-1-0)/(0.318)=(-1)/(0.318)=-3.144`

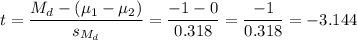
The degrees of freedom for this test are:

`df=n_1+n_2-1=12+14-2=24`

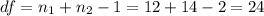
The critical value for a significance level of 0.05, a two tailed test with 4 degrees of freedom is t=±2.064.

This test is a two-tailed test, with 24 degrees of freedom and t=-3.144, so the P-value for this test is calculated as (using a t-table):

`P-value=2\cdot P(t<-3.144)=0.004`

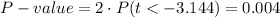
As the P-value (0.004) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the two processes yield different average errors.