Question

The inverse demand curve a monopoly faces isp= 130 - QThe firms cost curve isC(q) = 40 + 5Q1. What is the profit Maximizing solution ?The​ profit-maximizing quantity is ______? ​(Round your answer to two decimal​ places.)The​ profit-maximizing price is ________​$ (round your answer to two decimal​ places.)2. What is the firms economic profit?The firm earns a profit of _____? ( round your answer to two decimal places)

Answer 1

62.50 units

$3,866.25

Step-by-step explanation:

The price function is:

`p = 130 - Q`

`C = 40+5Q`

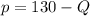
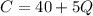
Profit as a function of quantity (P(Q)) is given by:

`P(Q) = Q*p(Q) - C(Q)\\P(Q) = Q*(130-Q)-40-5Q\\P(Q) = -Q^2+125Q-40`

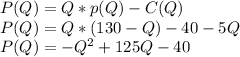
The quantity for which the derivate of the profit function is zero is the profit maximizing quantity:

`P(Q) = -Q^2+125Q-40\\P'(Q) =0= -2Q+125\\Q=62.50\ units`

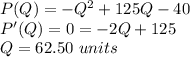
The​ profit-maximizing quantity is 62.50 units

The economic profit for this production volume is:

`P(62.5) = -(62.5^2)+125*62.5-40\\P(62.5)=\$3,866.25`

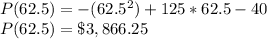
The firm earns a profit of $3,866.25.