Question

The San Francisco football team plays better in fair weather. They have a 70% chance of winning in good weather but only a 20% chance of winning in bad weather. (a) If they play in the Super Bowl in Wisconsin and the weatherman predicts a 60% chance of snow that day, what is the probability that San Francisco will win. (b) Given that San Francisco lost, what is the probability that the weather was bad

Answer 1

a) 40% probability that San Francisco will win.

b) 80% probability that the weather was bad

Explanation:

In this problem, there are these following probabilities:

60% probability of bad weather.

If there is bad weather, 20% probability of SF winning.

100-60 = 40% chance of good weather.

If there is good weather, 70% probability of SF winning.

(a) If they play in the Super Bowl in Wisconsin and the weatherman predicts a 60% chance of snow that day, what is the probability that San Francisco will win.

If it snows, 20% probability of winning. If it does not snow, 70% probability of winning.

0.2*0.6 + 0.7*0.4 = 0.4

40% probability that San Francisco will win.

b) Given that San Francisco lost, what is the probability that the weather was bad:

Conditional probability:

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

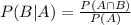
In which

P(B|A) is the probability of event B happening, given that A happened.

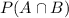`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: SF losing

Event B: Bad weather

P(A):

Probability of SF losing, which from a), is 0.6 = 60%.

P(A and B)

60% chance of snow. If it snows, 80% probability of SF losing. So

`P(A \cap B) = 0.6*0.8 = 0.48`

Then

`P(B|A) = (0.48)/(0.60) = 0.8`

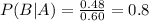
80% probability that the weather was bad