Question

1. Find the ratio of the areas of two similar triangles if the ratio of similitude is:

a) 2:1
b) 1:9
C: 3:5
2. Find the ratio of two corresponding sides of two similar polygons if the ratio of
areas is:
a) 4:9
b) 16:25
c) 49:256
3. The lengths of the diameters of two circles are 6 and 10. Find the following
ratios:
a) the ratio of their radii
b) the ratio of their circumferences
c) the ratio of their areas

Answer 1

1. (a)4:1 (b)1:81 (c)9:25

2. (a)2:3 (b)4;5 (c)7:16

3. (a)3:5 (b)3:5 (c)9:25

Explanation:

1. Given the ratio of similitude of two similar triangles, the ratio of their areas is the square of the ratio of similitude.

(a)2:1

Ratio of Area

`=2^2:1^2\\=4:1`

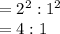
(b)1:9

Ratio of Area

`=1^2:9^2\\=1:81`

(c)3:5

Ratio of Area

`=3^2:5^2\\=9:25`

2. Given the ratio of the areas of the sides of two similar polygons, the ratio of the sides is the ratio of the square root of their areas.

(a)4:9

Ratio of Sides
`=√(4) :√(9)=2:3`

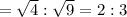
(b)16:25

Ratio of Sides
`=√(16) :√(25)=4:5`

(c)49:256

Ratio of Sides
`=√(49) :√(256)=7:16`

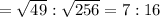
3.Lengths of the Diameter are 6 and 10.

Diameter = Radius/2

Therefore, their radii are 3 and 5.

(a)Ratio of their Radii =3:5

(b)Since the circumference is still a length, Ratio of their Circumference =3:5

(c)Ratio of their Areas

`=3^2:5^2\\=9:25`