Question

An electronic system has three major circuit boards, A, B and C. These boards have respective software support in the ratio, (30 %) : (30 %) : (40 %). Further, percentages of software failure observed in A, B and C respectively are: (4 %), (5 %) and (3 %). Suppose a random failure is observed. What is the probability that this failure is from A, B or C?

Answer 1

30.77% probability that this failure is from A.

38.46% probability that this failure is from B.

30.77% probability that this failure is from C.

Explanation:

Conditional probability:

`P(B|A) = (P(A \cap B))/(P(A))`

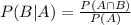
In which

P(B|A) is the probability of event B happening, given that A happened.

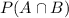`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

30% probability of board A being chosen.

Board A has a 4% probability of failure.

30% probability of board B being chosen.

Board B has a 5% probability of failure.

40% probability of board C being chosen.

Board B has a 3% probability of failure.

For all these questions:

Event A: Failure

So

`P(A) = 0.3*0.04 + 0.3*0.05 + 0.4*0.03 = 0.039`

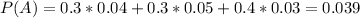
Probability that this failure is from A:

Event B: Board A is chosen.

Intersection:

Failure from board A:

`P(A \cap B) = 0.3*0.04 = 0.012`

`P(B|A) = (P(A \cap B))/(P(A)) = (0.012)/(0.039) = 0.3077`

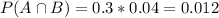
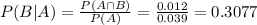
30.77% probability that this failure is from A.

Probability that this failure is from B:

Event B: Board B is chosen.

Intersection:

Failure from board B:

`P(A \cap B) = 0.3*0.05 = 0.015`

`P(B|A) = (P(A \cap B))/(P(A)) = (0.015)/(0.039) = 0.3846`

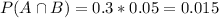
38.46% probability that this failure is from B.

Probability that this failure is from C:

Event B: Board C is chosen.

Intersection:

Failure from board C:

`P(A \cap B) = 0.4*0.03 = 0.012`

`P(B|A) = (P(A \cap B))/(P(A)) = (0.012)/(0.039) = 0.3077`

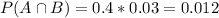
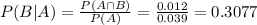
30.77% probability that this failure is from C.