Question

Coherent light with wavelength 610 nm passes through two very narrow slits, and the interference pattern is observed on a screen a distance of 3.00 m from the slits. The first-order bright fringe is a distance of 4.84 mm from the center of the central bright fringe. Part A For what wavelength of light will the first-order dark fringe (the first dark fringe next to a central maximum) be observed at this same point on the screen

Answer 1

Step-by-step explanation:

Wavelength of light λ = 610 nm

Screen distance D = 3.00 m

Slit separation be d

position of first bright fringe = λ D / d

Putting the values given

4.84 x 10⁻³ =
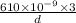
`(610*10^(-9)*3)/(d)`

d =
`(610*10^(-9)*3)/(4.84*10^(-3))`

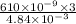
= 378.1 x 10⁻⁶ m

Let the required wave length be λ₁

Equation for position of dark fringe is given by following relation

x =
`((2n+1)\lambda* D)/(2d)`

Putting the value in the equation

4.84 x 10⁻³ =
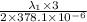`(\lambda_1* 3 )/(2*378.1*10^(-6))` , for first dark fringe n = 0

λ₁ = 1220 x 10⁻⁹

= 1220 nm .