Answer:
Yes, the triangle is a right triangle.
Explanation:
A triangle with a base of 8 meters and longest side is 17 meters.
Area of triangle is
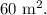
Let third side be x m
Semi-perimeter of triangle,
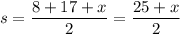
Using Heron's formula to find area of triangle.

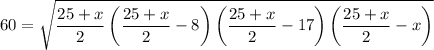
squaring both sides
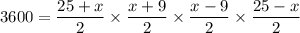
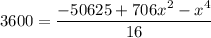

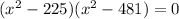
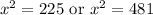
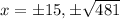
x should be positive integer.
So,
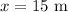
Using pthagoreous theorem:
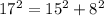
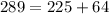
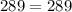
Therefore, the given triangle is a right triangle.