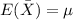Answer:
1)

And the margin of error for this case is
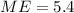
And the confidence interval would be:
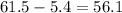
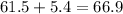
2) For this case the best estimator for the population mean
 is given by the sample mean:
is given by the sample mean:
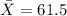
And the reason of this is beacuse is an unbiased estimator of the parameter:
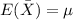
Explanation:
Data given:
53.1, 60.2, 60.6, 62.1, 64.4, 68.6.
We can calculate the sample mean with the following formula:

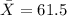 represent the sample mean for the sample
represent the sample mean for the sample
 population mean (variable of interest)
population mean (variable of interest)
s represent the sample standard deviation
n represent the sample size
Part 1
The confidence interval for the mean is given by the following formula:
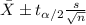 (1)
(1)
Or equivalently:

And the margin of error for this case is
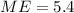
And the confidence interval would be:
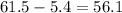
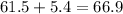
Part 2
For this case the best estimator for the population mean
 is given by the sample mean:
is given by the sample mean:
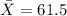
And the reason of this is beacuse is an unbiased estimator of the parameter: