Answer: The original concentration of copper sulfate is 0.56 g/L
Step-by-step explanation:
To calculate the number of moles, we use the equation:
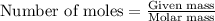 .....(1)
.....(1)
Given mass of copper = 89 mg = 0.089 g (Conversion factor: 1 g = 1000 mg)
Molar mass of copper = 63.5 g/mol
Putting values in equation 1, we get:
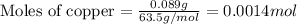
The given chemical equation follows:

By Stoichiometry of the reaction:
1 mole of copper metal is produced by 1 mole of copper sulfate
So, 0.0014 moles of copper metal will be produced by =
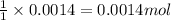 of copper sulfate
of copper sulfate
Now, calculating the mass of copper sulfate from equation 1, we get:
Molar mass of copper sulfate = 159.6 g/mol
Moles of copper sulfate = 0.0014 moles
Putting values in equation 1, we get:

- Calculating the original concentration of copper sulfate:
Mass of copper sulfate = 0.223 g
Volume of copper sulfate = 400 mL = 0.400 L (Conversion factor: 1 L = 1000 mL)
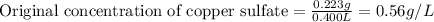
Hence, the original concentration of copper sulfate is 0.56 g/L