Question

A market research firm used a sample of individuals to rate the purchase potential of a particular product before and after the individuals saw a new television commercial about the product. The purchase potential ratings were based on a 0 to 10 scale, with higher values indicating a higher purchase potential. The null hypothesis stated that the mean rating "after" would be less than or equal to the mean rating "before." Rejection of this hypothesis would show that the commercial improved the mean purchase potential rating. Use α = 0.05 and the following data to test the hypothesis and comment on the value of the commercial. Individual Purchase Rating After Before 1 6 5 2 6 4 3 7 7 4 4 3 5 3 5 6 9 8 7 7 5 8 6 6

Answer 1

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the commercial improved the mean purchase potential rating.

Explanation:

If we calculate the difference in ratings we have:

After Before Difference

1 6 -5

5 2 3

6 4 2

3 7 -4

7 4 3

4 3 1

5 3 2

5 6 -1

9 8 1

7 7 0

5 8 -3

6 6 0

We will calculate the mean and standard deviation of the difference to test them later.

The sample size is n=12.

The mean is:

`M=(1)/(12)\sum_(i=1)^(12)((-5)+3+2+(-4)+3+1+2+(-1)+1+0+(-3)+0)\\\\\\ M=(-1)/(12)=-0.083`

The standard deviation is:

`s=\sqrt{(1)/((n-1))\sum_(i=1)^(12)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(11)\cdot [(-5-(-0.083))^2+(3-(-0.083))^2+...+(0-(-0.083))^2]}\\\\\\`

`s=\sqrt{(1)/(11)\cdot [(24.17)+(9.51)+...+(1.17)+(0.01)+(8.51)+(0.01)]}\\\\\\s=\sqrt{(78.92)/(11)}=√(7.174)\\\\\\s=2.678`

The null hypothesis states that the mean rating "after" would be less than or equal to the mean rating "before." The alternative hypothesis states that the mean rating difference is greater than 0.

Then, the null and alternative hypothesis:

`H_0: \mu\leq0\\\\H_a:\mu> 0`

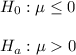
The significance level is 0.05.

The sample has a size n=12.

The sample difference is d=-0.083.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=2.678.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(2.678)/(√(12))=0.773`

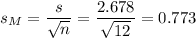
Then, we can calculate the t-statistic as:

`t=(\bar d)/(s/√(n))=(-0.083)/(0.773)=-0.108`

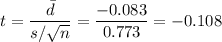
The degrees of freedom for this sample size are:

`df=n-1=12-1=11`

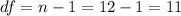
This test is a right-tailed test, with 11 degrees of freedom and t=-0.108, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t>-0.108)=0.542`

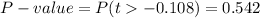
As the P-value is greater than the significance level, the effect is not significant. The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the commercial improved the mean purchase potential rating.