Answer:
Explanation:
Hello!
The variable Y: pH of the water of a stream that feeds into Lake Travis (stream A, stream B, and stream C)
This is a one way ANOVA with one factor (ph of the water) and three levels (stream A, stream B, and stream C).
a)
The parameters of interest are the population mean of pH of each stream, then the hypotheses for this ANOVA are
H₀: μ
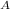 =μ
=μ
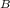 =μ
=μ
 =μ
=μ
H₁: At least one population mean is not equal to the others.
b)
There are many factors that may change the pH of water, for example:
1) Polution
2) Soil components (different concentrations of minearls) and pH of the soil
c)
The null hypothesis was rejected, so they made a post-hoc analysis to see wich of the population means is different from the others:
Using the same α: 0.05 as before
The deicsion rule for the p-value approach is
If p-value ≤ α, reject the null hypothesis.
If p-value ≥ α, do not reject the null hypothesis
1.
Stream A vs. B: p = 0.003
H₀: μ
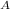 =μ
=μ
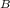
H₁: μ
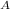 ≠μ
≠μ
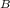
p-value: 0.003 < α: 0.05 ⇒ Reject null hypothesis. The average pH of stream A is different than the average pH of stream B.
2.
Stream A vs. C: p= 0.029
H₀: μ
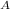 =μ
=μ

H₁: μ
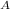 ≠μ
≠μ

p-value: 0.029 < α: 0.05 ⇒ Reject null hypothesis. The average pH of stream A is different than the average pH of stream C.
3.
Stream A vs. C: p= 0.041
H₀: μ
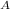 =μ
=μ

H₁: μ
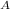 ≠μ
≠μ

p-value: 0.041 < α: 0.05 ⇒ Reject null hypothesis. The average pH of stream A is different than the average pH of stream C.
I hope this helps!