Answer:
- 379.48 s ( specific impulse )
- 3678.75 m/s ( exit velocity )
- 263.21 kg/s ( mass flow )
- 979855.3 N ( thrust )
- 0.168
 ( throat area )
( throat area )
Step-by-step explanation:
A) Specific impulse
standard altitude = 25 km
take free steam pressure (
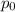 ) = 2527.3 N/
) = 2527.3 N/

Exit pressure = ambient pressure. therefore exit pressure (
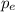 ) = 2527.3 N/
) = 2527.3 N/

Applying specific impulse equation
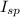 =
=
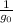 [
[
![(2Y T_(0) )/(Y - 1) ((R)/(M) )[ 1 - ((P_(e) )/(p_(0) ))^{(y-1)/(1) } ]]^{(1)/(2) }](https://img.qammunity.org/2021/formulas/engineering/college/pjz969jrzm5v0y0actx9rryl1ghn123wg1.png) equation 1
equation 1
given
 = 9.81 m/
= 9.81 m/
 , M = 20 kg/kmol, R = 8314.47 j/kmol.k
, M = 20 kg/kmol, R = 8314.47 j/kmol.k
y = 1.18,
 = 3756 k,
= 3756 k,
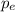 = 2527.3 N/
= 2527.3 N/
 ,
,
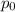 = 30 atm
= 30 atm
substitute the given data into equation 1
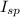 ( specific impulse ) = 379.48 s
( specific impulse ) = 379.48 s
B) exit velocity
Relating the equation for isentropic process, pressure and temperature at the combustion chamber , the exit temperature (Te) can be calculated using this formula :
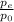 =
=

SUBSTITUTE the value of the above parameters
make (Te) subject of the equation Te = 1273.11 k
next calculate for constant specific pressure ( Cp )
Cp =
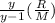
substitute the value of the above parameters into the equation
Cp = 2725.3 J/kg.k
Finally with Te and Cp known calculate the exit velocity
Ve =
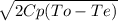
Cp = 2725.3 J/kg.k
To = 3756 k
Te = 1273.11 k
substitute the given values into the equation
Ve = 3678.75 m/s ( exit velocity )
C ) Mass flow
firstly calculate the density of the gas at exit ( De )
De =
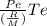
substituting the values of the parameters into the equation
De ( density of gas at exit ) = 0.00477 kg/m

finally calculate the Mass flow at the exit
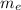 = De*Ve*Ae
= De*Ve*Ae
De = 0.00477 kg/

Ve = 3678.75 m/s
Ae = 15

therefore
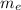 = 263.21 kg/s
= 263.21 kg/s
D ) thrust
calculate the weight flow rate rate ( w ) firstly
w = mg ( mass flow * speed of gravity )
= 263.21 * 9.81 = 2582.1 N/s
finally calculate thrust by applying this equation for thrust
T ( thrust ) = specific impulse * weight flow rate
= 379.48 * 2582. 1 = 979855.3 N
E ) throat area
calculate the throat area using this equation
m =
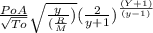
substituting the values of : m , M , R, To, y, and Po into the equation and making A subject of the equation
A =
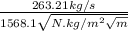 = 0.168
= 0.168
 ( throat area )
( throat area )