Answer:
(a)
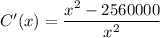
(b)x=1600, Minimum Average Cost Per iPod=$132
(c)
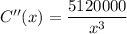
The result, C''(1600) is positive, which means that the average cost is Concave up at the critical point, and the critical point is a minimum.
Explanation:
Given that it costs Apple approximately $ C(x) to manufacture x 32GB iPods in a day, where:
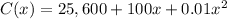
(a)The average cost per iPod when they manufacture x iPods in a day is given by:
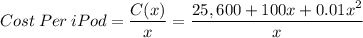
The average cost per iPod is therefore:
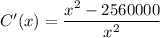
(b)To minimize average cost of x iPods per day, we set the average cost per iPod=0 and solve for x.
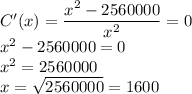
The resulting minimum average cost (at x=1600) is given as:

Second derivative test
(c)The answer above is a critical point for the average cost function. To show it is a minimum, we calculate the second derivative of the average cost function.
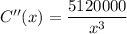
At the critical point, x=1600
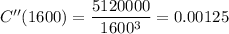
The result, C''(1600) is positive, which means that the average cost is Concave up at the critical point, and the critical point is a minimum.