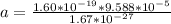Answer:
The acceleration is

Step-by-step explanation:
From the question we are told that
The radius of the cylinder is

The magnitude of the magnetic field is
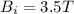
The rate of decrease is
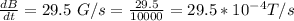
The distance from the center is
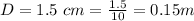
Faraday's law of induction states mathematically that
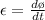
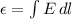
Where
 is the induced emf
is the induced emf
E is the magnitude of the electric field
 i the change in length
i the change in length
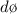 is the change in magnetic flux which is mathematically represented as
is the change in magnetic flux which is mathematically represented as
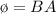
substituting this into the above equation
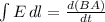
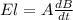
Where l is the circumference of the circular loop formed in the cylinder which is mathematically represented as
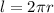
And A is the area of the circular loop formed which is mathematically represented as
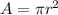
So
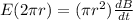
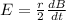
Substituting value
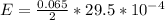

Generally acceleration is mathematically represented as
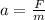
Now F is the electric force which is mathematically represented as
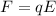
Substituting this into the question
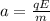
Where q is the charge on the proton with a constant value of
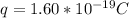
and m is the mass of the proton with a constant value of
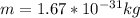
Substituting values