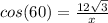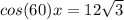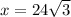Answer:
11)
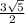
12)
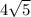
13)
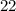
14)
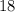
15)

16)

Step-by-step explanation:
For these problems I used the pythagorean theorem:
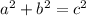 and SOHCAHTOA
and SOHCAHTOA
Sin =

Cos =

Tan =

11)
First find the length of the bottom side by using Cos
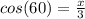
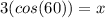
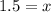
Then plug it into the formula for the pythagorean theorem to find the hypotenuse

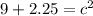
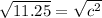
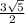
12)
Find the length of the bottom side using Cos
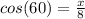

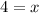
Then plug it into the formula for the pythagorean theorem to find the hypotenuse

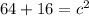
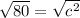
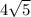
13)
Find the length of the other side by using Tan
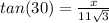
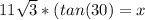
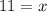
Then plug it into the formula for the pythagorean theorem to find the hypotenuse
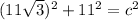
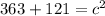
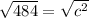
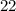
14)
(This is probably an easier way to do these problems)
Find the hypotenuse by using Cos (
 )
)
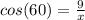
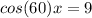
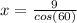

15)
Find the hypotenuse using Sin (
 )
)
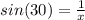
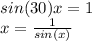

16)
Find the hypotenuse using Cos (
 )
)