Question

A catfish is 1.5 m below the surface of a smooth lake.

(a) What is the diameter of the circle on the surface through which the fish can see the world outside the water?
(b) If the fish descends, does the diameter of the circle increase, decrease, or remain the same? Assume that the index of refraction of water is 1.333.

Answer 1

A. The diameter of the circle would be 3.4 m

B. As the fish descends the diameter would increase.

Step-by-step explanation:

Part A

The critical angle can be obtained with the expression below;

Sin θ = 1/n

given n is the refractive index = 1.333

sinθ = 1/1.333

θ =
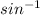`sin^(-1)` ( 1/1.333)

θ = 48.75
`3^(0)`

Therefore the critical angle would be θ = 48.75
`3^(0)`

from the diagram attached the sine of the critical angle can be evaluated thus;

Remember tan θ = Opposite / adjacent

From our diagram the radius r is the opposite, the adjacent is the 1.5 m depth. Therefore the tan of the critical angle would be;

tan θ = r/1.5

Tan 48.75
`3^(0)` = r/ 1.5

1.1404 = r / 1.5

r = 1.1404 x 1.5

r = 1.7106 m

Since the radius is 1.7106 m the diameter would be;

D = r x 2

D = 1.7106 x 2

D = 3.4212 m

D ≈ 3.4 m

Therefore the diameter of the circle would be 3.4 m

Part B

Since the fish is descending at a constant critical angle and same refractive index. There would be an increase in the adjacent resulting in a corresponding increase in the opposite which represents the diameter.

Therefore as the fish descends the diameter would increase.