Question

The profit that a vendor makes per day by selling x elephant ears is given by the function P(x)= -0.004x^2+3.2x-200. Find the number of elephant ears that must be sold to maximize profit. To maximize profit elephant ears must be sold

Answer 1

The number of elephant ears that must be sold to maximize profit is 400.

Explanation:

Given that,

The profit that a vendor makes per day is given by

P(x)= - 0.004x² +3.2 x -200

where x is number of elephant ears.

P(x)= - 0.004x² +3.2 x -200

Differentiating with respect to x

P'(x)= - 0.008x+3.2

Again differentiating with respect to x

P''(x) = -0.008

For maximum or minimum P'(x)=0

- 0.008x+3.2=0

⇒0.008x=3.2

`\Rightarrow x=(3.2)/(0.008)`

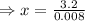
⇒ x = 400

`P''(x)|_(x=400) = -0.008<0`

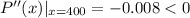
Since at x=400, P''(x)<0, the profit is maximize.

P(400) = -0.004×400²+3.2×400-200

=440

The number of elephant ears that must be sold to maximize profit is 400.