Answer:
No, there is not enough evidence to support the claim that true average task time with armor is less than 2 seconds.
Explanation:
This is a hypothesis test for the population mean.
The claim is that true average task time with armor is less than 2 seconds.
Then, the null and alternative hypothesis are:
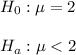
The significance level is 0.01.
The sample has a size n=52.
The sample mean is M=1.95.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=0.2.
The estimated standard error of the mean is computed using the formula:
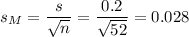
Then, we can calculate the t-statistic as:
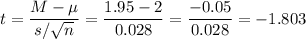
The degrees of freedom for this sample size are:
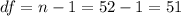
This test is a left-tailed test, with 51 degrees of freedom and t=-1.803, so the P-value for this test is calculated as (using a t-table):
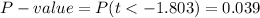
As the P-value (0.039) is bigger than the significance level (0.01), the effect is not significant.
The null hypothesis failed to be rejected.
There is not enough evidence to support the claim that true average task time with armor is less than 2 seconds.