Question

Mr. Jones has insomnia once a week.If he had an insomnia, he will definitely drink a cup of coffee in the morning. If he got a good night sleep, he will drink coffee with probability 1/2. Let I be the event that he has insomnia. Let C be the event that he drinks coffee in the morning. Given the information above: P(I) = 1/7, P(C|I) = 1 and P(C|I) = 1/2.

Find probability that he drinks coffee in the morning.

Answer 1

`P(C)=(4)/(7)`

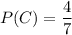
Explanation:

Given:

I is the event that he has insomnia.

C is the event that he drinks coffee in the morning.

`P(I) = (1)/(7) , P(C|I) = 1 ,and \:P(C|I^c) = (1)/(2)`

`P(I^c)=1-P(I) =1- (1)/(7)=(6)/(7)`

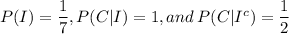
We want to determine the probability that he drinks coffee in the morning, P(C).

Using the Law of Total Probability

`P(C)=P(I)P(C|I)+P(I^c)P(C|I^c)`

`=(1)/(7)*1+(6)/(7)*(1)/(2)\\=(1)/(7)+(3)/(7)\\P(C)=(4)/(7)`

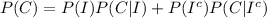
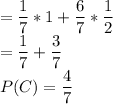
The probability that he drinks coffee in the morning is
`(4)/(7)`