Question

"Immediately after a ban on using hand-held cell phones while driving was implemented, compliance with the law was measured. A random sample of 1,250 drivers found that 98.9% were in compliance. A year after the implementation, compliance was again measured to see if compliance was the same (or not) as previously measured. A different random sample of 1,100 drivers found 96.9% compliance."

a. State an appropriate null and alternative hypothesis for testing whether or not there is any statistical difference in these two proportions measured initially and then one year later.
b. Conduct the test of hypothesis you stated in part a). Be sure to check the conditions for your test. State the P-value of your test and your conclusion.

Answer 1

(a) Null Hypothesis,
`H_0` :
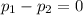`p_1-p_2=0` or
`p_1= p_2`

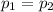
Alternate Hypothesis,
`H_A` :
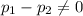`p_1-p_2\\eq 0` or
`p_1\\eq p_2`

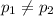
(b) We conclude that there is a statistical difference in these two proportions measured initially and then one year later.

Explanation:

We are given that a random sample of 1,250 drivers found that 98.9% were in compliance. A year after the implementation, compliance was again measured to see if compliance was the same (or not) as previously measured.

A different random sample of 1,100 drivers found 96.9% compliance."

Let
`p_1` = proportion of drivers that were in compliance initially

`p_2` = proportion of drivers that were in compliance one year later

(a) Null Hypothesis,
`H_0` :
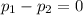`p_1-p_2=0` or
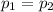`p_1= p_2` {means that there is not any statistical difference in these two proportions measured initially and then one year later}

Alternate Hypothesis,
`H_A` :
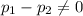`p_1-p_2\\eq 0` or
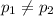`p_1\\eq p_2` {means that there is a statistical difference in these two proportions measured initially and then one year later}

The test statistics that will be used here is Two-sample z proportion statistics;

T.S. =
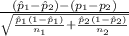`\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{ (\hat p_1(1-\hat p_1))/(n_1) + (\hat p_2(1-\hat p_2))/(n_2)} }` ~ N(0,1)

where,
`\hat p_1` = sample proportion of drivers in compliance initially = 98.9%

`\hat p_2` = sample proportion of drivers in compliance one year later = 96.9%

`n_1` = sample of drivers initially = 1,250

`n_2` = sample of drivers one year later = 1,100

(b) So, the test statistics =
`\frac{(0.989-0.969)-(0)}{\sqrt{ (0.989(1-0.989))/(1,250) + (0.969(1-0.969))/(1,100)} }`

= 3.33

Now, P-value of the test statistics is given by;

P-value = P(Z > 3.33) = 1 - P(Z
`\leq` 3.33)

= 1 - 0.99957 = 0.00043

Since in the question we are not given with the level of significance so we assume it to be 5%. Now at 5% significance level, the z table gives critical values between -1.96 and 1.96 for two-tailed test.

Since our test statistics does not lies within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that there is a statistical difference in these two proportions measured initially and then one year later.