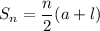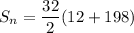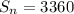Question

(Answered myself, I did this for others gain since it wasn't on this site)

Answer each question about the following arithmetic series:

12 + 18 + 24 + 30 + . . . + 198


1.) What is the explicit rule for the arithmetic sequence on which the series is based?
2.) How many terms are in the series?
3.) What is the value of the arithmetic series?

ANSWERS:
1.)
`a_(n) = 12+(n-1)6`

2.) n = 32

3.) C. 3,360

Answer 1

1.) an= 12 + (n-1) 6

2.) n = 32

3.) C. 3,360

Explanation:

Answer 2

Given series,

12 + 18 + 24 + 30 + . . . + 198

first term of series, a = 12

common difference,d = 18- 12 = 6

Last term of the series, a_n or l = 198.

a) The expression of arithmetic sequence given by the explicit rule is

`a_n = a + (n-1)d`

`a_n = 12 + (n-1)6`

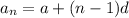
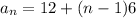
b) number of terms in the series

`198 = 12 + (n-1)6`

`n-1 = 31`

`n = 32`

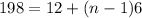
c) value of the series

`S_n = (n)/(2)(a+l)`

`S_n = (32)/(2)(12+198)`

`S_n = 3360`