Question

A mobile virtual reality (VR) headset is being sold at a local department store for $33.75. This is the cost function associated with the headsets, where x represents the number of headsets manufactured and sold: C(x) = 28.15x + 355. How many VR headsets does the store need to sell to break even?

Answer 1

B. 64

Explanation:

$33.75 x 64 = $2160

$28.15 x 64 + $355 = $2156.60

$2160 > $2156.60

Therefore the store is beyond breaking even, and they are $3.40 in the green.

Answer 2

63 headsets.

Explanation:

It is given that, a mobile virtual reality (VR) headset is being sold at a local department store for $33.75.

Let x represents the number of headsets manufactured and sold.

So, the revenue function is

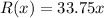`R(x)=33.75x` ...(i)

The given cost function is

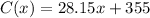`C(x)=28.15x+355` ...(ii)

In break even point the value of profit is zero. It means revenue and cost are equal.

`R(x)=C(x)`

`33.75x=28.15x+355`

`33.75x-28.15x=355`

`5.6x=355`

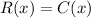
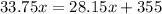
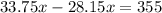
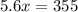
Divide both sides by 5.6.

`x=(355)/(5.6)`

`x\approx 63.393`

`x\approx 63`

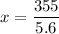
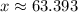
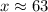
Therefore, the store need to sell 63 headsets.