Answer:
The best option is;
A triangle with three equal sides all longer than 12 inches
Explanation:
The cross sectional area of the square prism that passes through points A, B and C is found as follows;
Shape of cross section ABC = Triangle
Base, AB of the triangle is given by;
AB = √(8² + 8²) = √128 = 8·√2
Side, AC of the triangle is given by AC = √(8² + 12²) = 4√13
Therefore, the height of the triangle is given as follows;
Height, h = √(4·√13)²-(4·√2)² = 4·√11
The area of the cross section then is 0.5 × Base × Height
= 0.5 × 8·√2 × 4·√11 = 16·√22
A triangle with 3 equal sides of 8 inches has an area of 4×8×sin(60) = 16√3
A triangle with 2 equal sides of 12 inches and one side of 8 inches has an area of 4×12×sin(60) = 24√3
Therefore since 16·√22 > 24√3 > 16√3, the best option is a triangle with three equal sides of
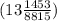all longer than 12 inches.