Answer:
The probability that a person is guilty given that he or she denies the knowledge of the error is 0.6068.
Explanation:
The Bayes' theorem states that the conditional probability of an event E
 , belonging to the sample space S, given that another event A has already occurred is:
, belonging to the sample space S, given that another event A has already occurred is:
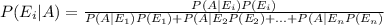
Denote the events as follows:
X = illegal deduction is filed
Y = knowledge of the error is denied.
The information given is:
P (Cheating) = 0.06
P (Actual error) = 0.03
P (Y|X) = 0.76
Compute the probability of X as follows:

The probability that a person who is not guilty will deny the knowledge of the error, is:
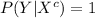
Compute the value of P (X|Y) as follows:
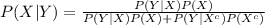

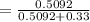
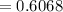
Thus, the probability that a person is guilty given that he or she denies the knowledge of the error is 0.6068.