Question

Saturated water with a quality of 0.55 and a temperature of 120 oC enters an uninsulated diffuser at a velocity of 180 m/s. The mass flow rate is 1.5 kg/s. If the water is to exit as saturated water vapor at a temperature of 120 oC, with negligible velocity, determine the necessary heat transfer rate.

Answer 1

`Q_(in)=146.22kW`

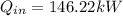
Step-by-step explanation:

Hello,

In this case, the energy balance for the given uninsulated diffuser is:

`m_(in)h_(in)+m_(in)(v_(in)^2)/(2)+Q_(in) =m_(out)h_(out)+m_(out)(v_(out)^2)/(2)`

Thus, we shall remember that the inlet mass equals the outlet mass and the outlet velocity is negligible, for that reason we obtain:

`mh_(in)+m(v_(in)^2)/(2)+Q_(in) =mh_(out)`

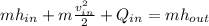
Hence, solving for the heat, we need the enthalpy at the inlet, which at 120°C for a liquid-vapor mixture results:

`h_(in)=503.81(kJ)/(kg) +0.55*2202.1(kJ)/(kg)=1714.965(kJ)/(kg)`

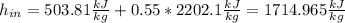
Moreover, at 120 °C the outlet enthlapy as saturated steam is:

`2706.0(kJ)/(kg)`

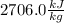
(Values extracted from Cengel, Thermodynamics 7th edition). In such a way, the required heat inlet is:

`Q_(in)=m(h_(out)-h_(in)-(v_(in)^2)/(2))=0.15(kg)/(s)(2706.0(kJ)/(kg)-1714.965(kJ)/(kg)-((180m/s)^2)/(2*1000))`

`Q_(in)=146.22kW`

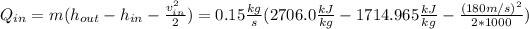
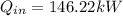
Notice that the term having the velocity should be divided by 1000 to obtain it in kJ/kg.

Best regards.