Answer:
The test statistic t = 3.61270
The tabulated value t₀.₀₅ = 3.61270 is greater than the tabulated value 2.4185 at 0.05 level of significance.
The null hypothesis is rejected at 0.05 level of significance.
the population means are not different
Explanation:
Step(i):-
Given first sample size 'n₁' = 19
Given the mean annual family income for 19 people making inquiries at the first development is $148,000, with a standard deviation of $41,000
The mean of first sample 'x₁⁻ ' = $148,000
The standard deviation of first sample S₁ = $41,000
Given data a corresponding sample of 25 people at the second development had a mean of $186,000, with a standard deviation of $27,000
The second sample size n₂ = 25
The mean of second sample 'x₂⁻ = $186,000
The standard deviation of first sample S₂ = $27,000
Step(ii) :-
Null hypothesis : H₀ : μ₁= μ₂
Alternative hypothesis :H₁: μ₁≠μ₂
Level of significance ∝ = 0.05
Degrees of freedom : ν = n₁+n₂-2 = 19+25-2 = 42
Test of hypothesis
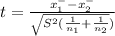
where
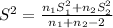
on calculation , we get
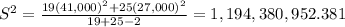

on calculation , we get
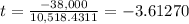
Taking modulus
|t| = |-3.61270|
t = 3.61270
Step(iii):-
The degrees of freedom ν = n₁+n₂-2 = 19+25-2 = 42
The tabulated value t₀.₀₅ = 3.61270 is greater than the tabulated value 2.4185 at 0.05 level of significance.
Conclusion:-
The null hypothesis is rejected at 0.05 level of significance.
we accepted alternative hypothesis that is H1:μ1 ≠ μ2
the population means are not different