Given that 4 is a zero of the polynomial function f left parenthesis x right parenthesis, find the remaining zeros. f left parenthesis x right parenthesisequalsx cubed minus 6 …

Question

asked Oct 27, 2021 206k views

1 Answer

Veeresh Honnaraddi · Answer 1 · 2021-11-01T12:07:33+0000

We have been given that 4 is a zero of the polynomial function
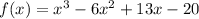f(x)=x^3-6x^2+13x-20 . We are asked to find the remaining zeros of function.

Since 4 is a zero of f(x), so
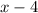x-4 will be a factor of f(x).

Let us divide our function f(x) by
x-4 .

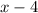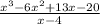
(x^3-6x^2+13x-20)/(x-4)

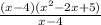
((x-4)(x^2-2x+5))/(x-4)

Now we will cancel out
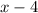x-4 from numerator and denominator.

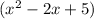
(x^2-2x+5)

Now we will use quadratic formula to solve for x as:

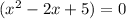
(x^2-2x+5)=0

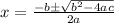
$x=(-b\pm√(b^2-4ac))/(2a)$

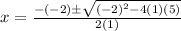
$x=(-(-2)\pm√((-2)^2-4(1)(5)))/(2(1))$

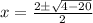
$x=(2\pm√(4-20))/(2)$

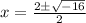
$x=(2\pm√(-16))/(2)$

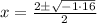
$x=(2\pm√(-1\cdot 16))/(2)$

Now we will use
i^2=-1 .

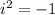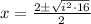
$x=(2\pm√(i^2\cdot 16))/(2)$

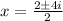
$x=(2\pm 4i)/(2)$

$x=(2(1\pm 2i))/(2)$

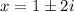
$x=1\pm 2i$

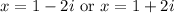
$x=1-2i\text{ or }x= 1+2i$

Therefore, other two zeros of function are
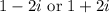$1-2i\text{ or } 1+2i$ .