Question

Consider a paint-drying situation in which drying time for a test specimen is normally distributed with σ = 7. The hypotheses H0: μ = 74 and Ha: μ < 74 are to be tested using a random sample of n = 25 observations. (a) How many standard deviations (of X) below the null value is x = 72.3? (b) If x = 72.3, what is the conclusion using a = 0.01?

Answer 1

(a) The value
`\bar x` = 72.3 is 1.21 standard deviations below the null value of μ.

(b) The mean drying time of paint is not less than 74.

Explanation:

The hypothesis for the single mean test is:

H₀: μ = 74 vs. Hₐ: μ < 74.

The information provided is:

σ = 7

n = 25

As the population standard deviation is known, we will use a z-test for single mean.

(a)

The z-score is a Normal distribution with mean 0 and variance 1. It is also defined as the number of standard deviations a raw score is from the mean.

The z-score for sample mean is given by:

`z=(\bar x-\mu)/(\sigma/√(n))`

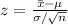
If
`\bar x` = 72.3 compute the corresponding z-score as follows:

`z=(\bar x-\mu)/(\sigma/√(n))`

`=(72.3-74)/(7/√(25))\\=-1.21`

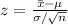
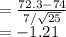
Thus, the value
`\bar x` = 72.3 is 1.21 standard deviations below the null value of μ.

(b)

So the test statistic is, z = -1.21.

Compute the p-value of the test as follows:

`p-value=P(Z<z)\\=P(Z<-1.21)\\=0.1131`

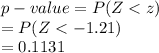
*Use a z-table.

The decision rule says to, reject the null hypothesis if the p-value is less than the significance level α = 0.01 and vice-versa.

p-value = 0.1131 < α = 0.01

The null hypothesis was failed to be rejected.

Thus, the mean drying time of paint is not less than 74.