Question

In the library on a university campus, there is a sign in the elevator that indicates a limit of 16 persons. Furthermore, there is a weight limit of 2500 lb. Assume that the average weight of students, faculty, and staff on campus is 149 lb, that the standard deviation is 28 lb, and that the distribution of weights of individuals on campus is approximately normal. If a random sample of 16 persons from the campus is to be taken:

(a) What is the expected value of the sample mean of their weights?
(b) What is the standard deviation of the sampling distribution of the sample mean weight? (Round your answer to two decimal places.)
(c) What average weights for a sample of 16 people will result in the total weight exceeding the weight limit of 2500 lb?
(d) What is the chance that a random sample of 16 persons on the elevator will exceed the weight limit? (Round your answer to four decimal places.)

Answer 1

a) 149 lb

b) 7 b

c) 156.25 lb

d) 0.1492 = 14.92% probability that a random sample of 16 persons on the elevator will exceed the weight limit

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

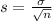For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this problem, we have that:

`\mu = 149, \sigma = 28, n = 16, s = (28)/(√(16)) = 7`

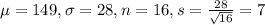
(a) What is the expected value of the sample mean of their weights?

By the Central Limit Theorem, 149 lb.

(b) What is the standard deviation of the sampling distribution of the sample mean weight? (Round your answer to two decimal places.)

By the Central Limit Theorem, 7 lb.

(c) What average weights for a sample of 16 people will result in the total weight exceeding the weight limit of 2500 lb?

In total, 16 people weighing 2500 lb.

2500/16 = 156.25 lb

Average weights of 156.25 lb will result in the total weight exceeding the weight limit of 2500 lb.

(d) What is the chance that a random sample of 16 persons on the elevator will exceed the weight limit?

This is 1 subtracted by the pvalue of Z when X = 16. So

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (156.25 - 149)/(7)`

`Z = 1.04`

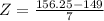
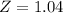
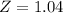`Z = 1.04` has a pvalue of 0.8508

1 - 0.8508 = 0.1492

0.1492 = 14.92% probability that a random sample of 16 persons on the elevator will exceed the weight limit