Answer:
the lost work per kilogram of water for this everyday household happening = 0.413 kJ/kg
Step-by-step explanation:
Given that:
Initial Temperature
 = 15°C
= 15°C
Initial Pressure
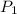 = 5 atm
= 5 atm
Final Pressure
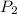 = 1 atm
= 1 atm
Data obtain from steam tables of saturated water at 15°C are as follows:
Specific volume v = 1.001 cm³/gm
The change in temperature = 2°C
Specific heat of water = 4.19 J/gm.K
volume expansivity β = 1.5 × 10⁻⁴ K⁻¹
The expression to determine the change in temperature can be given as :
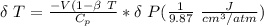

Δ T = 0.093 K
Now; we can calculate the lost work bt the formula:

where ;
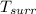 is the temperature of the surrounding. = 20°C = (20+273.15)K = 293.15 K
is the temperature of the surrounding. = 20°C = (20+273.15)K = 293.15 K
From above the change in entropy is:
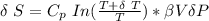
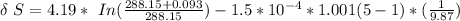
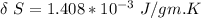

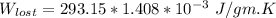
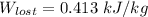
Thus, the lost work per kilogram of water for this everyday household happening = 0.413 kJ/kg