Question

A manufacturing process produces semiconductor chips with a known failure rate of . If a random sample of chips is selected, approximate the probability that at least will be defective. Use the normal approximation to the binomial with a correction for continuity

Answer 1

The probability that at least 14 of the chips will be defective is 0.6664.

Explanation:

The complete question is:

A manufacturing process produces semiconductor chips with a known failure rate of 5.4%. If a random sample of 300 chips is selected, approximate the probability that at least 14 will be defective. Use the normal approximation to the binomial with a correction for continuity .

Solution:

Let X = number of defective chips.

The probability that a chip is defective is, p = 0.054.

A random sample of n = 300 chips is selected.

A chip is defective or not is independent of the other chips.

The random variable X follows a Binomial distribution with parameters n = 300 and p = 0.054.

But the sample selected is too large.

So a Normal approximation to binomial can be applied to approximate the distribution of X if the following conditions are satisfied:

1. np ≥ 10
2. n(1 - p) ≥ 10

Check the conditions as follows:

`np=300* 0.054=16.2>10\\n(1-p)=300* (1-0.054)=283.8>10`

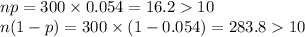
Thus, a Normal approximation to binomial can be applied.

So,
`X\sim N(\mu =16.2,\ \sigma^(2)=15.3252)`.

Compute the probability that at least 14 of the 300 chips will be defective as follows:

Use continuity correction:

P (X ≥ 14) = P (X > 14 + 0.50)

= P (X > 14.50)

`=P((X-\mu)/(\sigma)>(14.50-16.20)/(√(15.3252)))`

`=P(Z>-0.43)\\=P(Z<0.43)\\=0.6664`

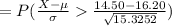
*Use a z-table for the probability.

Thus, the probability that at least 14 of the chips will be defective is 0.6664.