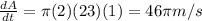Question

(a) If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of dr/dt.

(b) Suppose oil spills from a ruptured tanker and spreads in a circular pattern. If the radius of the oil spill increases at a constant rate of 1 m/s, how fast is the area of the spill increasing when the radius is 23 m?

Answer 1

a)
`(dA)/(dt) = \pi 2r (dr)/(dt)`

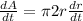
b) area of the spill increasing when the radius is 23 m

`(dA)/(dt) = 46\pi m/s`

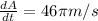
Step-by-step explanation:

Step-by-step explanation:-

a)

Given 'A' is the area of a circle with radius 'r'

The area of the circle
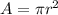`A = \pi r^(2)` ..(I)

Differentiating equation (I) with respective to 't'

`(dA)/(dt) = \pi 2r (dr)/(dt)`

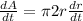
b)

If the radius of the oil spill increases at a constant rate of 1 m/s

Given the radius r= 23m

Area of the spill increasing when the radius is 23 m

`(dA)/(dt) = \pi (2)(23) (1) =46\pi m/s`