Question

A 5 kg wooden block sitson a flat straight-away12 meters fromthe bottom of an infinitely long ramp, which has an angle of 20 degrees. The straightaway has a coefficient of kinetic friction of 0.4and the ramp of 0.25. While the block is on the flat section, you exert a 100 N forceat an angle of 45 degrees above the horizontal, propelling the block towards the ramp.

a.What is the velocity of the block right before it begins going up the ramp?

b.How far up the ramp (the distance along the hypotenuse) does the block travel before stopping?

Answer 1

(a) 19.71801m/s Velocity just before going up the ramp.

(b) 74.56338m.

Step-by-step explanation:

We will solve it in two parts, first we will calculate time that 5kg wooden block would take to just reach ramp and with this time we will calculate final velocity that the wooden block would have in this time.

Second, we will calculate the component of velocity vector along inclined plane and the time that it would take for velocity to be 0 meters/s then with this time we will calculate the distance that inclined plane would travel along inclined plane.

Following formulas will be used.

`x(t) = (1)/(2) t^2 = 12m =16.2m/s^2 t^2`

`F =ma`

`V(t) = V_(o) +at`

`x(t) = x_(0) +v_(0)t+(1)/(2)a t^2`

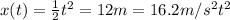
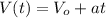
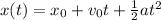
(a) Calculating velocity right before going up the ramp.

Wooden block is going on a straightaway and has net for on it.

`F_(n) =F-F_(s) = F-uF_(n) = 100N-0.4*9.8m/s^2*5kg` =
`81N`

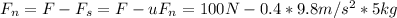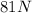
and this force produces acceleration of

`a = (F)/(m)=(81)/(5) =16.2m/s^2 .`

With this acceleration, wooden block would reach at the foot of ramp in.

`x(t) = 12m = 16.2m/s^2*t^2`

`t = 1.217s`

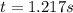
and final velocity will be

`v(t) = v_(0)+at = 0+16.2m/s^2*1.2171s = 19.7180m/s.`

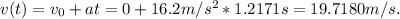
this velocity of wooden box just before going up the ramp.

(b) How far up the ramp will the wooden block go before stopping.

Ramp is at 20° relative to horizontal therefore velocity along the ramp that the wooden block would have will be.

`V= V_(h)cos(20) = 18.5288m/s`

and deceleration along the ramp is

`a = (F_(s) )/(m)`

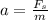
Where
`F_(s)` force of friction along the inclined plane.

`F_s = uF_n = u*m*a`

`a = 9.8m/s^2*cos(20) = 9.2089m/s^2`

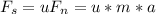
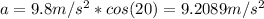
is a component of g along normal of the inclined plane.

`F_(s) = 0.25*5kg*9.2089m/s^2`

`= 11.5112N`

`a = (11.5112N)/(5kg) = 2.3022m/s^2`

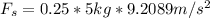
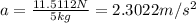
And with this deceleration time needed to get wooded block to stop is.

`v(t) = v_o-at = 18.5288m/s-2.3022m/s^2*t = 0`

`t = (18.5288m/s)/(2.3022m/s^2) =8.04813s`

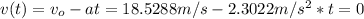
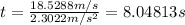
and in that time wooden block would travel

`x(8.04813s) = 18.52881m/s *8.04813s-\frac{1}{} 2.3022m/s^2*(8.0481)^2=74.56338m`

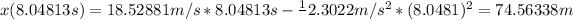
This is how up wooden box will go before coming to stop.