Question

The Online department was asked by the CEO to estimate the cost of crime to customers of Online. The department began their study with the crime of identity theft, taking a random sample of files (there is too much crime to calculate the statistics for all the crimes committed). They found the average dollar loss in an identity theft was $7000, with a standard deviation of $2000, and that the dollar loss was normally distributed. (Use this information for the following 3 questions. Again, calculate a z-score, and then use a table or app to figure out the percentage above/below/between the z-score. Some apps will do it all for you if you enter the mean and standard deviation.) In this sample, taken from Home Depot Online this week:

a) What proportion of identity thefts had dollar losses below $5000?

b) In the same sample above, what percentage of identity thefts have dollar losses between $10,000 and $12,000? (Explain/show how you obtain your answer.)

c) Find the dollar value for which only for 0.00135 of losses are as high or higher. (Explain/show how you obtain your answer.)

Answer 1

a) P(X>5,000) = 0.1587

b) P(10,000<X<12,000) = 0.0606

c) X = $13,000

Explanation:

As no sample size is informed, we assumed that the mean and standard deviation refers to the population of dollar loss in an identity theft.

Then, we can calculate the probabilities for this distribution transforming the values to a z-score and using the standarized normal distribution table to calculate the probabilities.

a) What proportion of identity thefts had dollar losses below $5000?

This is P(X<5000). As the mean is 7000 and the standard deviationis 2000, the z-score can be calculated as:

`z=(X-\mu)/(\sigma)=(5000-7000)/(2000)=(-2000)/(2000)=-1`

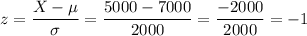
The probability for this z-score is

`P(X<5000)=P(z<-1)=0.1587`

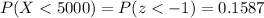
b) We can calculate the probability of X being between 10,000 and 12,000 calculating a z-score for each value.

Then, the interval is transformed to calculate the larger area P(X<12,000) and substract from it the smaller area P(X<10,000).

We first calculate the z-scores:

`z_1=(X_1-\mu)/(\sigma)=(10000-7000)/(2000)=(3000)/(2000)=1.5\\\\\\z=(X-\mu)/(\sigma)=(12000-7000)/(2000)=(5000)/(2000)=2.5`

Then we can calculate the probability as:

`P(10,000<X<12,000)=P(X<12,000)-P(X<10,000)\\\\\\P(10,000<X<12,000)=P(z<2.5)-P(z<1.5)\\\\ P(10,000<X<12,000)= 0.9938-0.9332=0.0606`

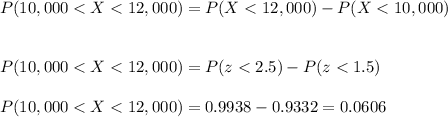
c) In this case, we know the probability, and we need to calculate the value X* for which P(X>X*)=0.00135.

We have to start by looking in a standard distribution for z such that P(z>z*)=0.00135.

This z is z*=3.

Then, we can calculate X from the z-score as:

`X^*=\mu+z^*\cdot \sigma=7,000+3*2,000=7,000+6,000=13,000`