Explanation:
We have, a sphere and a cylinder have the same radius and height. The volume of the cylinder,
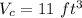
The volume of sphere is :
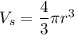
The volume of cylinder is :
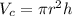
Dividing the volume of sphere and the volume and cylinder, such that,
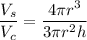
As r = h
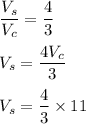
So, the volume of sphere is (four-third) of 11. therefore, the correct option is (A).