Answer:
C
Step-by-step explanation: The standard form of an exponential equation is
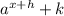
where a is the vertical dilation, h is the horinzontial translation, and k is the vertical translation.
Lets go through these options step by step.
A. In an exponetial equation, when k>1, the graph is translated upwards vertically. However, k could still be positive and doesn't be the shape of the picture of the graph always.
Plus our exponential function has an horinzontial asymptote at y=-4 so k here is negative, not positive.
B. When a<0, the graph end behavior changes. When a>1, the right side of the graph approaches infinity while the left side approaches an asymptote. However, when a<0, the graph could be two things. One ( when a< -1) could be that the right side approaches negative infinity, and the left side approaches asymptote. The other could be that (when -1<a<0) that the right side approaches an asymptote and the left side approaches negative infinity. In this function, this models a traditional exponetial function, when a is greater than 1 so B/D is Wrong.
C is correct, when a>1, the end behavior for the right side is infinity, and for the left side is some asymptote.