Question

The reference desk of a university library receives requests for assistance. Assume that a Poisson probability distribution with an arrival rate of 7 requests per hour can be used to describe the arrival pattern and that service times follow an exponential probability distribution with a service rate of 8 requests per hour.

A. What is the probability that no requests for assistance are in the system?
B. What is the average number of requests that will be waiting for service?
C. What is the average time in minutes before service begins?
D. What is the average time at the reference desk in minutes (waiting time plus service time)?
E. What is the probability that a new arrival has to wait for service?

Answer 1

a) 0.125

b) 7

c) 0.875 hr

d) 1 hr

e) 0.875

Step-by-step explanation:l

Given:

Arrival rate, λ = 7

Service rate, μ = 8

a) probability that no requests for assistance are in the system (system is idle).

Let's first find p.

a) ρ = λ/μ

`(7)/(8) = 0.875`

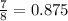
Probability that the system is idle =

1 - p

= 1 - 0.875

=0.125

probability that no requests for assistance are in the system is 0.125

b) average number of requests that will be waiting for service will be given as:

λ/(μ - λ)

`= (7)/(8 - 7)`

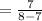
= 7

(c) Average time in minutes before service

= λ/[μ(μ - λ)]

`= (7)/(8(8 - 7))`

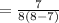
= 0.875 hour

(d) average time at the reference desk in minutes.

Average time in the system js given as: 1/(μ - λ)

`= (1)/((8 - 7))`

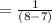
= 1 hour

(e) Probability that a new arrival has to wait for service will be:

λ/μ =

`{7}{8}`

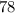
= 0.875