Question

Thirty-seven percent of all Americans drink bottled water more than once a week (Natural resources Defense Council, December 4, 2015). Suppose you have been hired by the Natural Resources Defence Council to investigate bottled water consumption in St. Paul. You plan to select a sample of St. Paulites to estimate the proportion who drink bottled water more than once a week. Assume the population proportion of St. Paulites who drink bottled water more than once a week is 0.37, the same as the overall proportion of Americans who drink bottled water more than once a week. Use z-table.

a. Suppose you select a sample of 540 St.Paulites. Show the sampling distribution of (p bar)(to 4 decimals).

b. Based upon a sample of 540 St. Paulites, what is the probability that the sample proportion will be within 0.09 of the population proportion (to 4 decimals).

probability =

d. Based upon a smaller sample of only 300 St. Paulites, what is the probability that the sample proportion will be within 0.09 of the population proportion (to 4 decimals).

probability =

e. As measured by the increase in probability, how much do you gain in precision by taking the larger sample in parts (a) and (b) rather than the smaller sample in parts (c) and (d)?

Answer 1

a) The sampling distribution for n=540 has a mean sample proportion of p=0.37 and a standard deviation of σs=0.0208.

b) probability = 0.99998

d) probability = 0.99874

e) You gain 0.12% in probability for an increase of 80% in sample size.

The increase in sample size is not justified by the increase in probability, for this margin of error (Δp=0.09).

Explanation:

a) We have a known population proportion π=0.37 and we have to describe the sampling distribution when the sample size is n=540.

The mean sample proportion is expected to be the same as the population proportion:

`\bar p = \pi = 0.37`

The standard deviation of the sampling will be the population standard deviation divided by the square root of the sample size:

`\sigma_s=(\sigma)/(√(n))=\sqrt{(p(1-p))/(n)}=\sqrt{(0.37*0.63)/(540)}=√(0.000431667)=0.0208`

Then, we can say that the sampling distribution will have a p=0.37 and a standard deviation σs=0.0208.

b) We have to calculate the probability that the sample proportion will be within 0.09 of the population proportion.

We can calculate the z-value as:

`z_1=(p_1-\bar p)/(\sigma_s)=(0.09)/(0.0208)=4.3269\\\\\\z_2=(p_2-\bar p)/(\sigma_s)=(-0.09)/(0.0208)=-4.3269`

As the distribution is symmetrical, we can calculate the probabilty that he sample proportion will be within 0.09 of the population proportion as:

`P(|p-\bar p|<0.09)=P(|z|<4.3269)=0.99998`

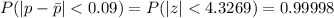
probability = 0.99998

d. Now the sample is smaller (n=300), so the standard deviation of the samping distribution:

`\sigma_s=(\sigma)/(√(n))=\sqrt{(p(1-p))/(n)}=\sqrt{(0.37*0.63)/(300)}=√(0.000777)=0.0279`

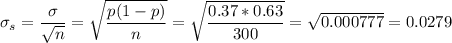
We have to recalculate the z-scores:

`z_1=(p_1-\bar p)/(\sigma_s)=(0.09)/(0.0279)=3.2258\\\\\\z_2=(p_2-\bar p)/(\sigma_s)=(-0.09)/(0.0279)=-3.2258`

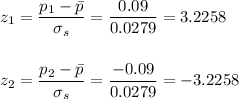
And the probability is:

`P(|p-\bar p|<0.09)=P(|z|<3.2258)=0.99874`

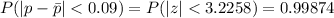
probability = 0.99874

e. The increase in sample size is 80%

`\Delta n\%=(n_1)/(n_2)-1=(540)/(300)-1=1.8-1=0.8=80\%`

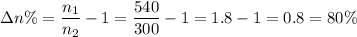
and the increase in probability is 0.12%

`\Delta P\%=(P_1)/(P_2)-1=(0.99998)/(0.99874)-1=1.0012-1=0.0012=0.12\%`

You gain 0.12% in probability for an increase of 80% in sample size.

The increase in sample size is not justified by the increase in probability, for this margin of error (Δp=0.09).