Question

Shankar really likes playing Badminton. On a particular day at Fetzer gym he plays two games (whose outcomes are independent of each other). He has .3 probability of winning the first game and he has .9 probability of winning the second game. There are no ties and as stated above the outcomes of each game are independent of each other. Let X denote the number of games shankar wins.

Calculate E[X] and E[X2].

Answer 1

E[X] = 1.2

E[X2] = 1.74

Explanation:

If X is the number of games shankar wins, the sample space for X is [0,1,2], as he can win none, on or the two games.

Let:

Pw1: probability of winning the first game

Pw2: probability of winning the second game

The probability of winning none of the games (X=0) is:

`P(X=0)=(1-Pw1)(1-Pw2)=(1-0.3)(1-0.9)=0.7*0.1=0.07`

The probability of winning only one of the games (X=1) is:

`P(X=1)=(1-Pw1)(Pw2)+(Pw1)(1-Pw2)=(1-0.3)(0.9)+(0.3)(1-0.9)\\\\P(X=1)=0.7*0.9+0.3*0.1=0.63+0.03=0.66`

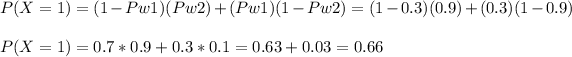
The probability of winning both games (X=2) is:

`P(X=2)=Pw1*Pw2=0.3*0.9=0.27`

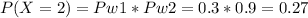
The expected value E(X) is:

`E(X)=\sum p_iX_i=0.07*0+0.66*1+0.27*2=0+0.66+0.54=1.2`

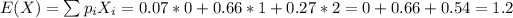
The expected value of the square of X, E(X^2) can be calculated as:

`E(X^2)=\sum p_iX_i^2=0.07*0^2+0.66*1^2+0.27*2^2\\\\E(X^2)=0+0.66*1+0.27*4=0.66+1.08=1.74`

Answer 2

Find the given attachment