Question

Wally wants to determine the height of a statue that casts a 164-inch shadow by comparing it to his own height and shadow length. If Wally, who is 68 inches tall, casts a shadow that is 41 inches in length, what is the height of the statue?

Answer 1

We have been given that Wally wants to determine the height of a statue that casts a 164-inch shadow by comparing it to his own height and shadow length. Wally is 68 inches tall, casts a shadow that is 41 inches in length.

We will use proportions to solve for the height of the statue because proportions state that ratio between two proportional quantities is same.

`\frac{\text{Height of statue}}{\text{Shadow of statue}}=\frac{\text{Height of Wally}}{\text{Shadow of Wally}}`

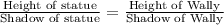
Upon substituting our given values in above equation, we will get:

`\frac{\text{Height of statue}}{\text{164 cm}}=\frac{\text{68 inch}}{\text{41 inch}}`

`\frac{\text{Height of statue}}{\text{164 cm}}* \text{164 cm}=\frac{\text{68 inch}}{\text{41 inch}}* \text{164 cm}`

`\text{Height of statue}=\frac{\text{68 inch}}{1}* 4`

`\text{Height of statue}=272\text{ inches}`

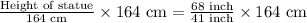
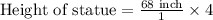
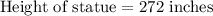
Therefore, the height of the statue is 272 inches.