Question

Mr. Jiménez has $10,000 to put into two different savings accounts. · Mr. Jiménez will deposit $4,000 into Account I, which earns 4.5% annual simple interest. · He will deposit $6,000 into Account II, which earns 4% interest compounded annually. Mr. Jiménez will make no additional deposits or withdrawals. What will be the total balance of these accounts at the end of 2 years?

Answer 1

We have been given that Mr. Jimenez has $10,000 to put into two different savings accounts. Mr. Jimenez will deposit $4,000 into Account I, which earns 4.5% annual simple interest. He will deposit $6,000 into Account II, which earns 4% interest compounded annually.

We are asked to find the total balance of these accounts at the end of 2 years.

We will use compound interest formula and simple interest formula to solve our given problem.

Simple interest formula:

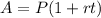`A=P(1+rt)`, where,

A = Final amount after t years,

P = Principal amount,

r = Annual interest rate in decimal form.

`4.5\%=(4.5)/(100)=0.045`

Let us find amount earned in 2 years at simple interest.

`A=\$4,000(1+0.045\cdot 2)`

`A=\$4,000(1+0.09)`

`A=\$4,000(1.09)`

`A=\$4360`

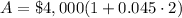
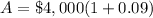
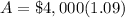
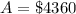
Now we will use compound interest formula.

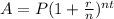`A=P(1+(r)/(n))^(nt)`, where, n represents number of times interest compounded per year.

`4\%=(4)/(100)=0.04`

`A=\$6,000(1+(0.04)/(1))^(1\cdot 2)`

`A=\$6,000(1+0.04)^2`

`A=\$6,000(1.0816)`

`A=\$6489.60`

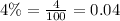
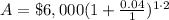
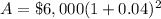
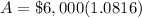
Let us add both amounts.

`\$6489.60+\$4360=\$10,849.60`

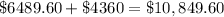
Therefore, the total balance of these accounts at the end of two years will be $10,849.60.