Question

Two objects, T and B, have identical size and shape and have uniform density. They are carefully placed in a container filled with a liquid. Both objects float in equilibrium. Less of object T is submerged than of object B, which floats, fully submerged, closer to the bottom of the container. Which of the following statements is true?

a. Object T has a greater density than object B.
b. Object B has a greater density than object T.
c. Both objects have the same density

Answer 1

b. Object B has a greater density than object T.

Step-by-step explanation:

When an object stay balance while submerged, its gravity must be the same as the buoyancy force, which is the same as the liquid weight displaced by the submerged volume:

`V_s\rho_lg = mg = V\rho_og`

`V_S\rho_l = V\rho_o`

`\rho_o = \rho_l(V_S)/(V)`

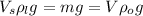
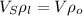
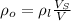
where
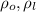`\rho_o, \rho_l` are densities of the object and liquid, respectively.
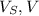`V_S, V` are the volume submerged and the object volume, respectively.

If object B is fully submerged then the density of object B is the same as the liquid density (because
`V_S / V = 1`).

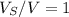As for object T as it's only partially submerged, the mass of the liquid displaced is same as mass of object. And while the volume displaced is only a portion of the whole object volume (
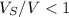`V_S / V < 1`), this means that the liquid density is greater than object T's density.

Therefore, object B has a greater density than object T.