Table 4 represents a linear function as the ratio of the change in y to the change in x is constant (
 ). The relationship is linear with a slope of
). The relationship is linear with a slope of
 .
.
A table represents a linear function if the ratio of the change in y to the change in x is constant. Let's check each table:
1. Table 1:
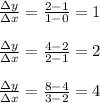
Since the ratio is not constant, Table 1 does not represent a linear function.
2. Table 2:
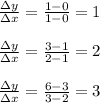
The ratio is not constant, so Table 2 does not represent a linear function.
3. Table 3:
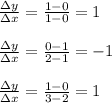
The ratio is not constant, so Table 3 does not represent a linear function.
4. Table 4:
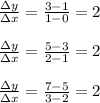
The ratio is constant at
 , so Table 4 represents a linear function.
, so Table 4 represents a linear function.